
LA FUERZA MAGNÉTICA SOBRE UNA CARGA EN MOVIMIENTO
En los artículos anteriores, hablamos sobre qué es el magnetismo, con su definición y sus propiedades. También hablamos sobre el campo magnético que se encuentra en los imanes y cómo modifica las propiedades del espacio.
En esta oportunidad hablaremos sobre las fuerzas magnéticas sobra cargas en movimiento, cómo influyen y sus principales características y fórmulas.
MAGNETISMO SOBRE CARGAS EN MOVIMIENTO
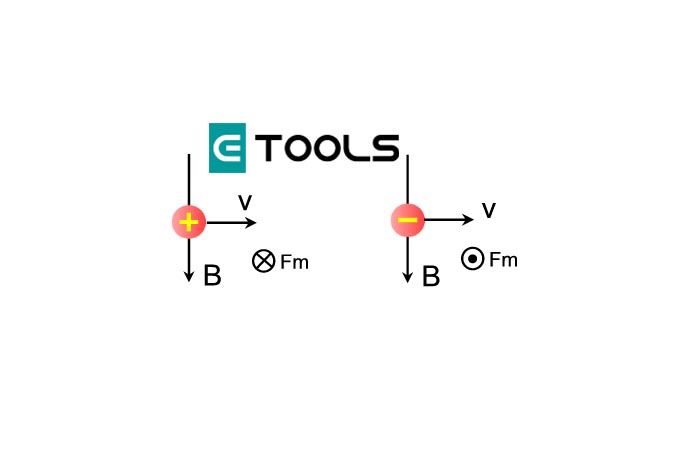
Acabamos de ver en el artículo anterior, que el pasaje de corriente afecta a un imán de la misma manera que la presencia de otro imán. Es decir que entre imanes aparecen fuerzas magnéticas y también aparecen fuerzas magnéticas entre una corriente (cargas en movimiento) y un imán. Es de esperar entonces que asimismo aparezcan fuerzas magnéticas entre cargas en movimiento o entre corrientes eléctricas o sobre cargas en movimiento en presencia de imanes. Estudiaremos ahora cómo es la fuerza magnética que aparece sobre una carga móvil cuando hay un campo magnético presente (ya sea producido por imanes o por corrientes). Las características de esta fuerza fueron determinadas experimentalmente estudiando el movimiento de partículas en presencia de campos magnéticos. Lo primero que podemos notar es que sobre partículas descargadas no aparece ninguna fuerza; eso es independiente de si las partículas se mueven o no. Esto significa que la fuerza magnética sobre una partícula depende de la carga eléctrica de la partícula. Otra cosa importante es que, si tenemos una partícula cargada en reposo en presencia de un campo magnético, tampoco aparecen fuerzas sobre ella. O sea, la presencia de un imán no afecta para nada a las cargas eléctricas mientras estas se encuentran en reposo. Esto indica que los campos magnéticos afectan a las partículas cargadas que están en movimiento, es decir, que tienen alguna velocidad. También se verifica que, cuando la velocidad de la partícula cargada resulta paralela a la dirección del campo magnético (en el mismo sentido o en el sentido contrario), no aparece ninguna fuerza magnética sobre la partícula. Eso es lo que se muestra en la figura para el caso de una partícula cargada moviéndose en un campo magnético constante y uniforme. Cuando la velocidad de la partícula forma un ángulo con la dirección del campo magnético, aparece la fuerza. Esta fuerza aumenta con el ángulo que forman la velocidad y el campo magnético y toma su valor máximo cuando el ángulo llega a los 90°, o sea, cuando la partícula se mueve en la dirección perpendicular al campo magnético. En suma, la intensidad de la fuerza magnética sobre una carga Q que se mueve con rapidez V en un campo magnético B se escribe de la siguiente manera:
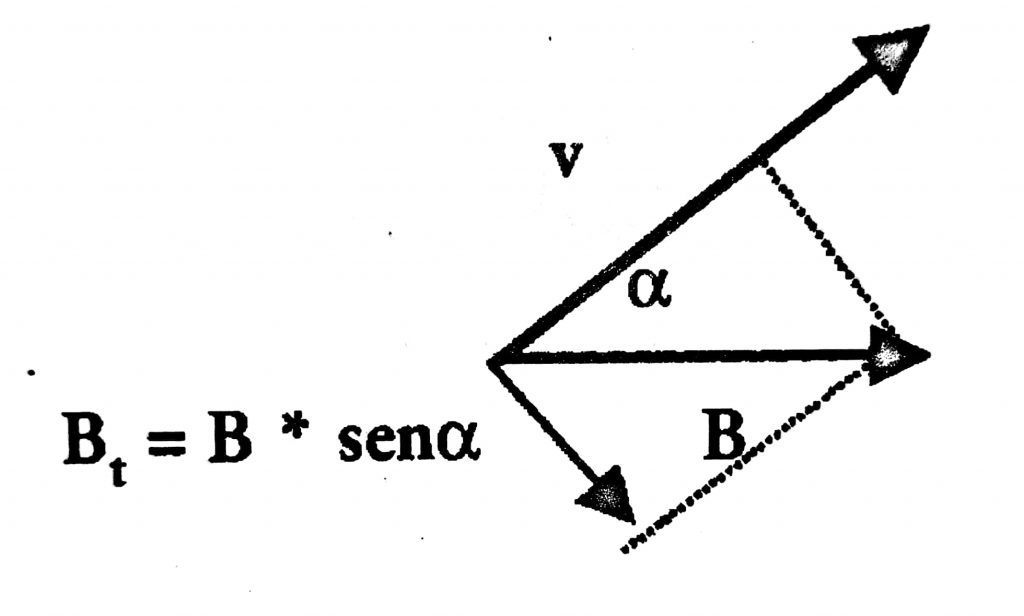
Viendo la imagen que se encuentra debajo de este párrafo, vemos que α es el ángulo entre la velocidad y el campo. La dirección de la fuerza magnética resulta perpendicular al plano definido por el vector velocidad V el vector campo magnético B. Es decir que la fuerza es perpendicular a ambos vectores, V y B. El sentido de la fuerza magnética está determinado por la regla de la mano derecha: ponemos la mano derecha plana, con los dedos extendidos. Luego apuntamos con el pulgar en la dirección en que se mueve la partícula. Orientamos los otros dedos en la dirección del campo magnético. En ese momento, la mano estará en el plano determinado por los dos vectores. El sentido de la fuerza magnética sobre una carga positiva es el que correspondería a dar una cachetada (si la carga es negativa, el sentido será opuesto). Hay una versión alternativa para esta regla: primero cerramos el puño. Después extendemos el pulgar y el índice. En ese momento, veremos que esos dedos forman una "L". Con el pulgar, indicamos la dirección de V, y con el índice, la dirección de B. Ahora extendemos el anular de manera perpendicular al pulgar y al índice. La fuerza magnética apuntará en la dirección que indica el dedo anular si la carga es positiva (si la carga es negativa, la fuerza magnética apuntará en el sentido opuesto).
Volviendo a ver la figura anterior, notamos que el producto B * senα es igual a la componente del campo magnético que resulta perpendicular a la velocidad B⊥. Esto nos permite expresar a la fuerza magnética con la siguiente fórmula:
Esta ecuación indica que las unidades de campo magnético son unidades de fuerza / (carga * velocidad). Si expresamos la carga en coulomb, la velocidad en metros/segundos y la fuerza en newton, B resultará expresado en la unidad internacional de campo magnético, denominada tesla (T) (en honor a Nicola Tesla, científico e inventor serbio). O sea:
Si éste y los anteriores artículos sobre magnetismo te han gustado y te han sido de utilidad o tiene más dudas sobre el tema, no dudes en dejarnos un comentario para seguir ayudándote y mejorando sobre los futuros temas.
Si quieres conocer otros artículos parecidos a LA FUERZA MAGNÉTICA SOBRE UNA CARGA EN MOVIMIENTO puedes visitar la categoría Fisica.
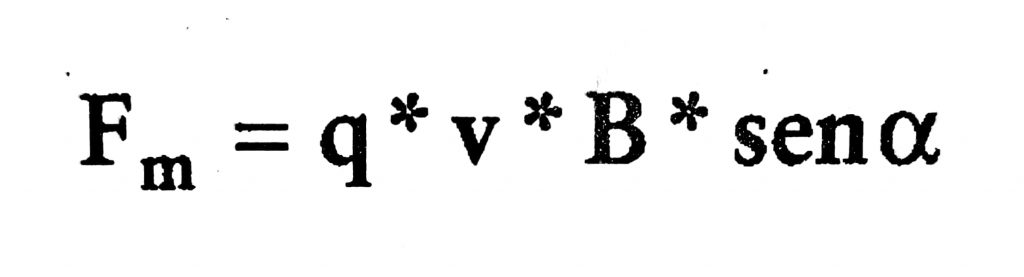
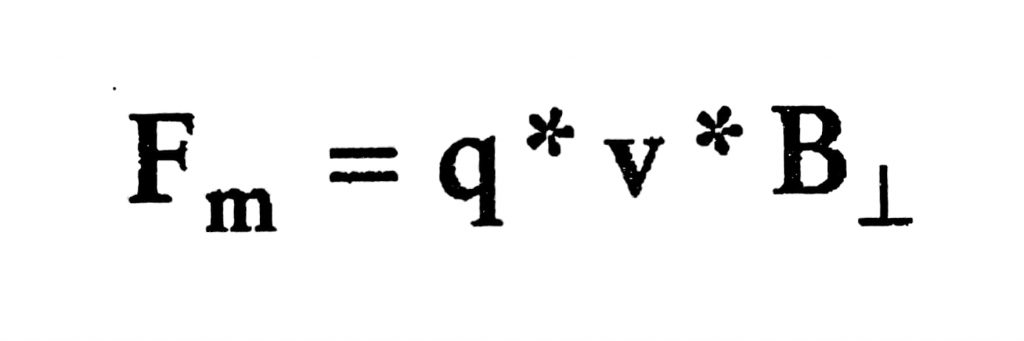
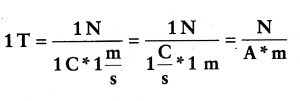





Deja un comentario