Ecuaciones de segundo grado ejercicios resueltos
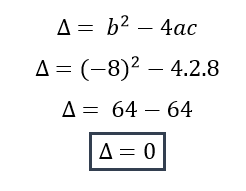
Las ecuaciones de segundo grado son aquellas que tienen la "X" elevada al cuadrado, formalmente se las conoce como funciones cuadráticas.
Antes de empezar a resolver problemas vamos a repasar un poco la teoría, que no viene nada mal a modo de recordatorio.
Marco Teórico
La forma general de la ecuación de segundo grado es la siguiente. 👇
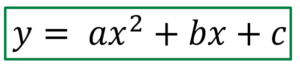
La única condición para que sea una ecuación de segundo grado es que a sea distinto de cero, para que no se anule el termino con "X" al cuadrado.
Si b o c son iguales a cero, decimos que es una ecuación de segundo grado incompleta.
Ecuación de segundo grado incompleta
Estas son las mas simples de resolver, por que hay menos términos involucrados, se pueden dar tres casos posibles.
Primer caso (a=0 y b=0 )
En esta situación, la única solución posible es cero, dado que la ecuación de segundo grado que lo representa es la siguiente.
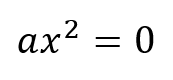
Segundo caso (solo c=0)
Cuando solo c es igual a cero. las soluciones posibles a la ecuación de segundo grado incompleta son las siguientes.
Tercer caso (solo b=0)
Cuando solo b es igual a cero. las soluciones posibles a la ecuación de segundo grado incompleta son las siguientes.
Ecuación de segundo grado completa
Se dice que la ecuación de segundo grado esta completa cuando a, b y c ≠ 0, y para encontrar las soluciones hay que aplicar la famosa formula resolvente. 👇
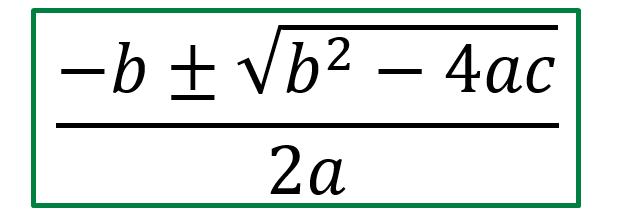
Discriminante
El discriminante de una ecuación de segundo grado es un indicador que nos permite conocer el tipo de solución que tiene la ecuación, antes de resolverla.
El signo del discriminante Δ nos indica el tipo de solución que tendrá la ecuación.

Ejercicios resueltos paso a paso
Vamos a resolver 10 ejercicios de ecuaciones de segundo grado, de menos a mayor complejidad.
Ejercicio 1
En la ecuación siguiente, determinar la cantidad de soluciones y las características de las mismas.
Para determinar la cantidad de soluciones que tiene tenemos que encontrar el determínate.
Como el discriminante es positivo entonces decimos que la ecuación de segundo grado tiene dos soluciones reales.
Ejercicio 2
En la ecuación siguiente, determinar la cantidad de soluciones y las características de las mismas.
Calculamos el discriminante
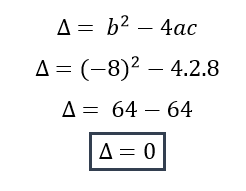
Como el discriminante es igual a cero entonces decimos que la ecuación de segundo grado tiene dos soluciones reales IGUALES.
Ejercicio 3
Resolver la siguiente ecuación de segundo grado incompleta.
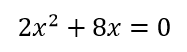
Es una ecuación de segundo grado por que el mayor exponente de la X es 2, y esta incompleta por que falta el termino independiente.
Para resolverlo simplemente tenemos que factorizar y nos queda una ecuación con la siguiente.
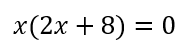
Esa ecuación da cero cuando x=0 y cuando x=-4. Dos soluciones reales y distintas.
Ejercicio 4
Encontrar los valores para los cuales la siguiente función corta al eje x.
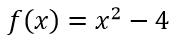
Tenemos que encontrar las raíces, para eso debemos igualar la función a cero y resolverla, en este caso estamos delante de una ecuación de segundo grado incompleta por que le falta el termino lineal.
La ecuación de segundo grado tiene dos soluciones reales DISTINTAS
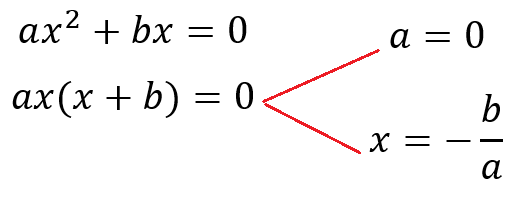
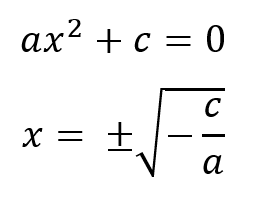
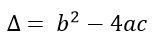
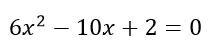
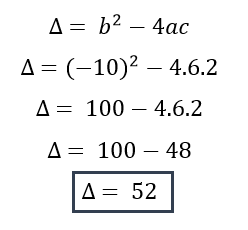
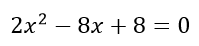
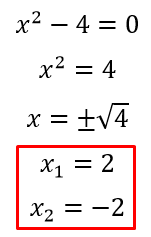
Deja un comentario