
Características de la Función cuadrática

Si esta leyendo esto seguramente estés en los primeros años del secundario ¿me equivoco? y como me paso a mi ni siquiera tengas del todo claro que es una función.
Así que bueno, antes de contarte las características de las funciones cuadráticas voy explicarte que es una función y despejes a tiempo esas dudas que si no te van a acompañar toda tu vida. 😉
▷ Definición de Funciones en Matemáticas
En el terreno de las matemáticas, se denomina función a la relación que existe entre dos conjuntos numéricos, donde uno dependa del otro, en términos etimológicos significa la relación "acción" y "efecto".
Dicho de otra manera, se dice que una magnitud es función de otra si el valor de la primera depende de la segunda.
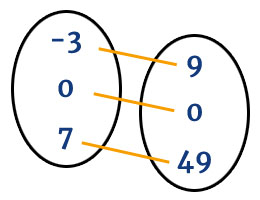
Un ejemplo gráfico seria el siguiente. 👇👇👇
Si se fijan, para las magnitudes del primer conjunto se corresponde una y solo una magnitud del segundo conjunto.
La función de la imagen anterior puede ser expresada matemáticamente según la siguiente ecuación.
Si nos fijamos y reemplazamos los valores del primer conjunto en x, nos va a dar como resultado en y el valor correspondiente al segundo conjunto.
- Si x = -3, y = 9
- Si x = 0, y = 0
- Si x = 7, y = 49
Ahora si, hablemos de funciones cuadráticas 👇🏻👇🏻
▷ Funciones cuadráticas - características
En matemáticas, hablamos de funciones cuadráticas cuando se puede expresar la ecuación mediante la siguiente forma. 👇🏻👇🏻
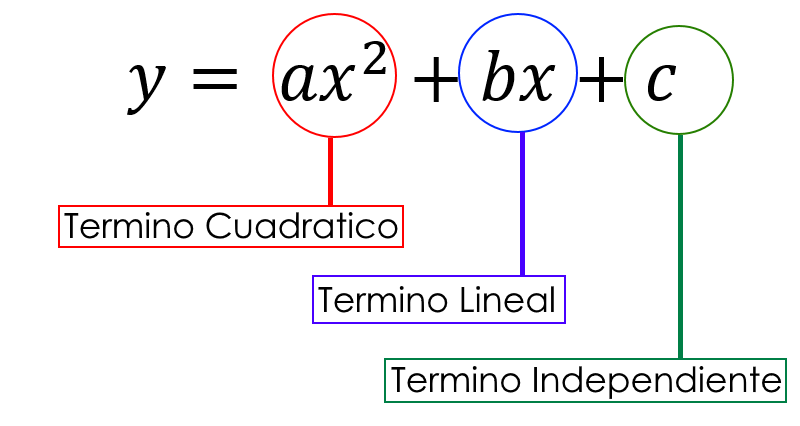
Como pueden ver, la ecuación cuenta con tres términos, cada termino tiene un nombre bien definido, se dice que la función esta completa cuando ninguno de estos términos es cero, si alguno fuera cero, la función cuadrática se dice que esta incompleta.
➛ Gráfica de una función cuadrática
La gráfica de una función cuadrática tiene una forma muy particular y importante que entiendas como se comporta o como varia según los términos que te comente antes.
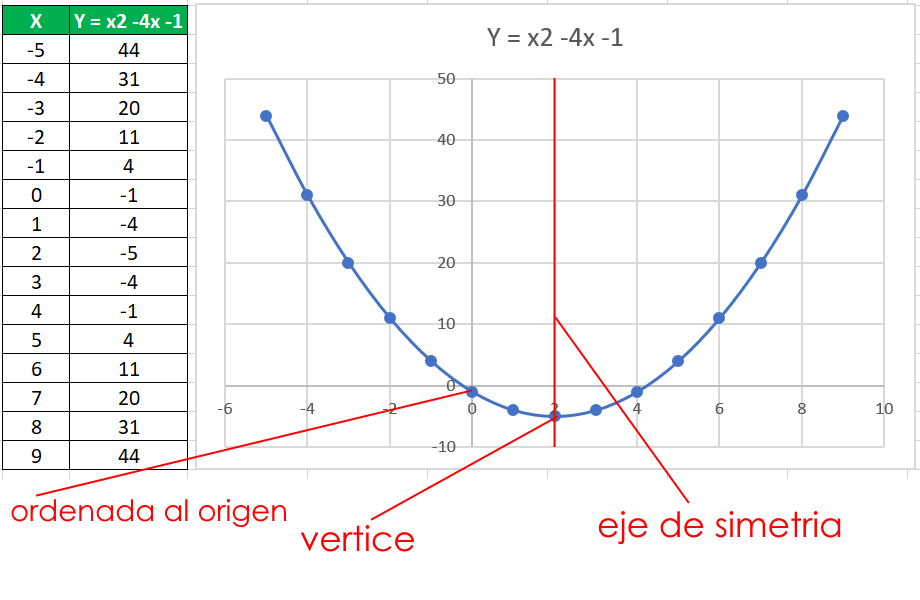
Toda función cuadrática tiene algunas características importantes de conocer, en la gráfica siguiente las marco en rojo, estas son Ordenada al origen - Vértice - y Eje de simetría.
La siguiente gráfica corresponde a la función x2 - 4x - 1
⇨ Ordenada al origen
La ordenada al origen de una función cuadrática es el valor que toma la función cuando x es igual a cero, gráficamente es la intersección de la función con el eje Y de coordenadas.
La forma de calcularlo es muy simple, es el valor de del termino independiente de la función.
⇨ Eje de simetría
El eje de simetría de una parábola o función cuadrática es una linea imaginaria que divide a la función en dos, esta linea siempre pasa por el vértice, se denomina eje de simetría por que parte a la función en forma simétrica.
⇨ Vértice de una función cuadrática
Acá si que no queda otra que hacer cuentas, para calcular el vértice de una función cuadrática tenemos que entender que este es un punto, y esta formado por dos componentes, una componente en Y y otra componente en X.
La siguiente formula nos da el valor de la coordenada x del vértice de la función (comúnmente se lo llama x del vértice)
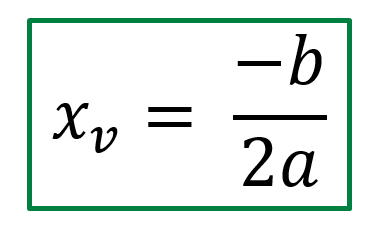
Para encontrar el Y del vértice hay que reemplazar el valor obtenido en la función de arriba en la parábola original.
⇨ Raíces de una función cuadrática
Se denominan raíces de una función cuadrática o parábola a los valores de x que hacen que la función sea cero.
Gráficamente se pueden ver cuando las "ramas" de la función cortan al eje x. Siguiendo el ejemplo de la gráfica de mas arriba, las raíces serian los puntos que recuadro en verde.
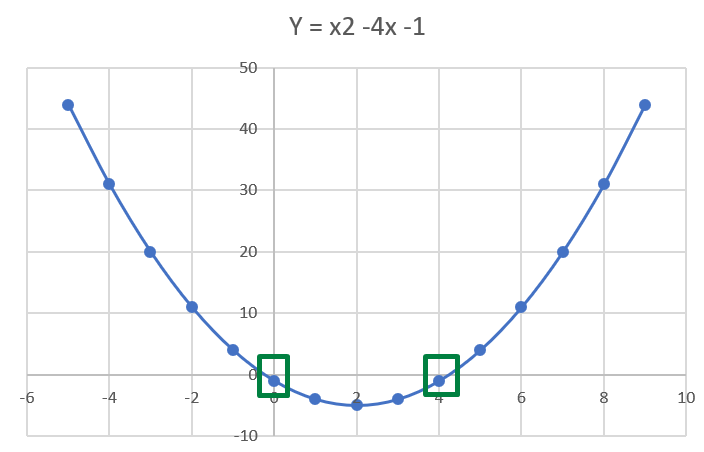
Ahora bien, que ya entendimos conceptualmente que son las raíces, la pregunta del millón... ¿Como se calculan las raíces de una función cuadrática? 👇👇
🔥 ¿Como se calculan las raíces de una función cuadrática?
Bueno, acá vamos a tener que hacer uso de una de las formulas mas conocidas en matemáticas, la famosa "formula resolvente" 👇
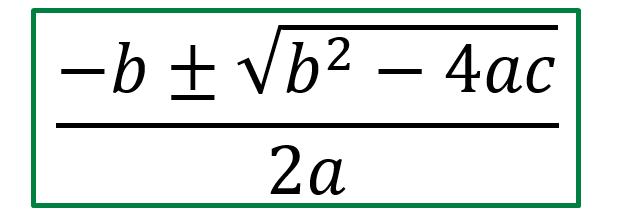
Esta función nos va a entregar dos resultados, ¿por que dos resultados?, bueno muy simple, como comente antes las raíces representan la intersección de las ramas de la parábola con el eje x, como son dos ramas.. entonces dos resultados.
¡Ojo! 👁👁 , pueden existir algunos casos donde los resultados de la formula resolvente sean números complejos, en ese caso se interpreta que la parábola nunca corta al eje X. Eso sucede cuando las ramas son positivas y el vértice esta por sobre el eje x.
Bueno, ahora que vimos la teoría de todo esto, vamos con un ejercicio resuelto. 👇🏻
▷ Ejercicios de función cuadrática
A veces, la mejor forma de entender y afianzar las ideas es trabajando con ejemplos, así que vamos a desarrollar el siguiente ejercicio resuelto.
➛ Ejercicio 1
Supongamos que tenemos la siguiente función cuadrática y nos piden calcular X del vértice e Y del vértice, las raíces y la ordenada al origen.
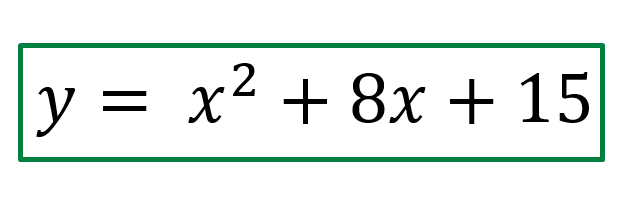
Lo primero que tenemos que hacer es identificar los valores a,b y c de la función cuadrática, en este ejemplo son los siguientes.
- a = 1 (el numero que multiplica a la x en el termino cuadrático)
- b = 8 (el numero que multiplica a la x en el termino lineal)
- c = 15 (el termino independiente)
⇨ Calcular X del Vértice
Para calcular X del vértice solo tenemos que aplicar la formula siguiente, donde tenemos que reemplazar los valor de a y b correspondientes.
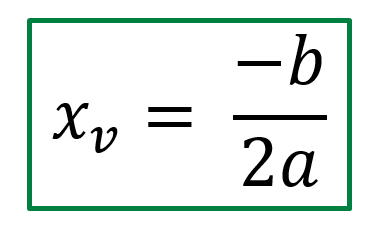
Con lo cual, el X del vértice de nuestra parábola es el siguiente. 👇🏻
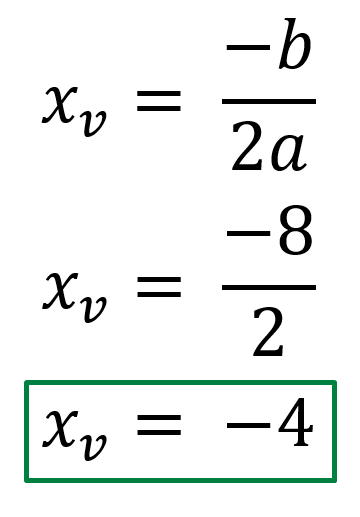
Ahora bien, para obtener el Y del vértice simplemente hay que reemplazar el valor del X del vértice en la función cuadrática.
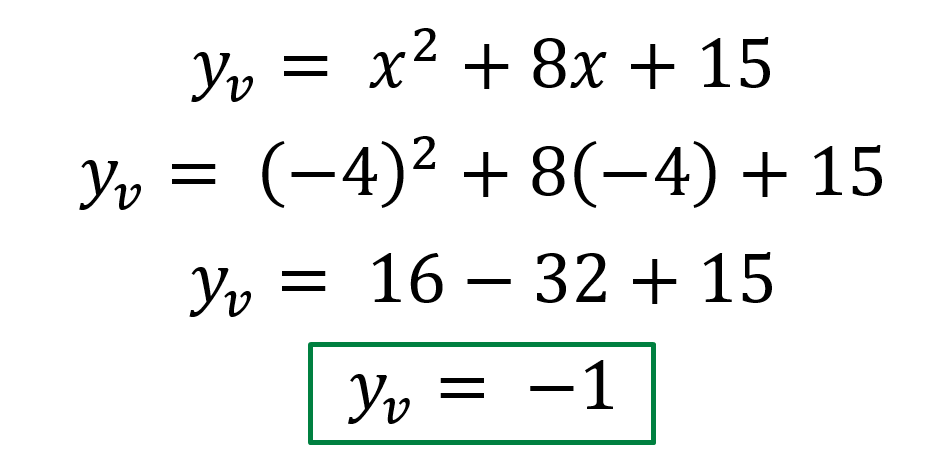
⇨ Raíces de la función cuadrática
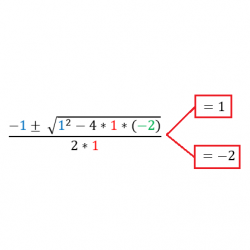
Acá tenemos que aplicar la formula cuadrática, la que comúnmente llamamos "formula resolvente", ya tenemos identificado del punto anterior los correspondientes valores de a, b y c así que solo tenemos que reemplazarlos en la formula.
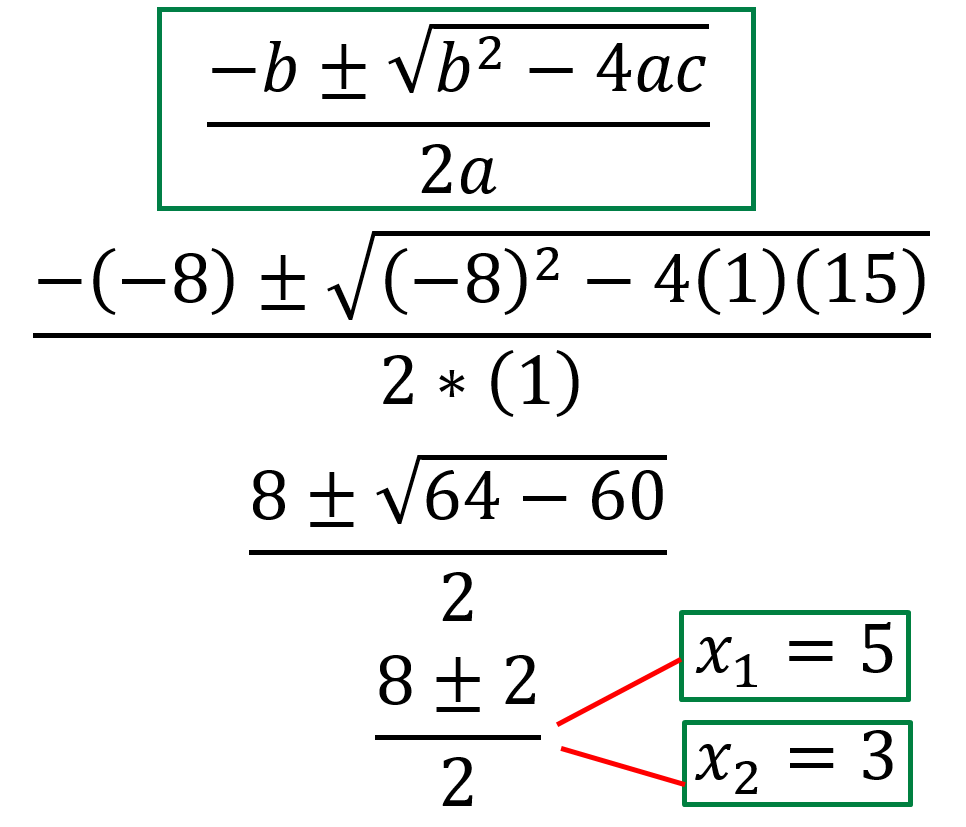
¿Que significan estos valores?, es muy simple y como dije anteriormente representan los valores de X donde las ramas cortan al eje X. Solo basta con graficar la función y ver que no nos equivocamos en los cálculos. 👇
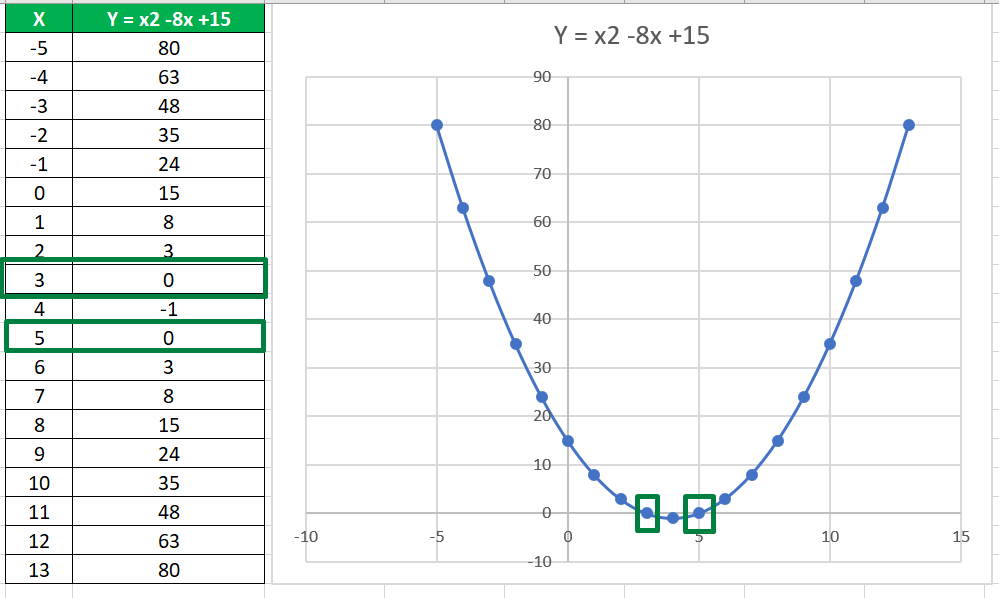
Quizás no se note del todo bien en la imagen de arriba, pero en los recuadros se puede ver que las ramas de la parábola cortan al eje X en los puntos que calculamos anteriormente.
▷ Vídeo Explicativo
Por si no quedo del todo claro la explicación les comparto un vídeo sobre lo mismo, espero que les sirva.
🙂
Si quieres conocer otros artículos parecidos a Características de la Función cuadrática puedes visitar la categoría Matemática básica.
-
-
Se resuelve remplazando la x en ax2+bx+c
-
Deja un comentario
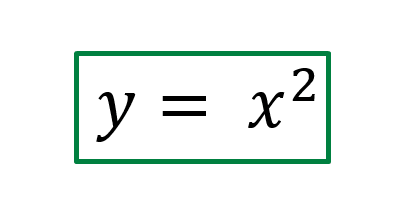
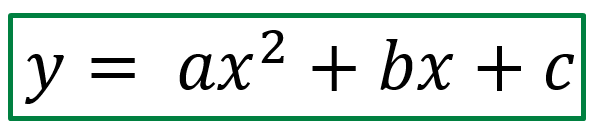

hola! los numeros(valores de Y) en la tabla, como se sacan? muchas gracias, me sirvio de mucho, aunque me quedo esa duda.