OPERACIONES CON NÚMEROS HEXADECIMALES
En el artículo anterior hablamos de los números hexadecimales, tanto su definición como el pasaje de un número hexadecimal a binario y decimal, como también la viceversa en ambos casos.
Ahora, daremos algunos ejemplos con distintos problemas para que, al terminar de leer, ya no te quede ninguna duda de cómo poder hacer la conversión sin ningún tipo de inconvenientes.
OPERACIONES CON NÚMEROS HEXADECIMALES
Suma de un número hexadecimal
- 8 + 8 = 16
Cómo el resultado no está entre el 0 y el 15, debemos de restar 16 al resultado y nos llevamos 1. Entonces
16 – 16 = 0; por lo tanto 8 + 8 será 10 (en el sistema hexadecimal)
- A + 8 = 18
Al igual que en el caso anterior, cómo el resultado supera el 15, debemos de restar 16. Por lo tanto
18 – 16 = 2; el resultado de A + 7 será 12 (hexadecimal)
- A + A = 20
Al igual que en los casos anteriores, debemos de restar 16
20 – 16 = 4; el resultado de A + A será 14 (hexadecimal)
- F + D = 28
Debemos de restar 16
28 – 16 = 12; por lo que el resultado de F + D será 1C (debemos tener cuidado de cuando utilizar las letras, ya que el 12 en hexadecimal es C)
Resta de un número hexadecimal
En la resta las cosas se complican un poco. Para poder realizar la resta de dos números hexadecimales debemos sumar al minuendo el complemento a la quince del sustraendo y, finalmente, sumarle 1 (el bit de overflow que desborda).
Aquí dejaremos un claro ejemplo de cómo se realiza la resta:
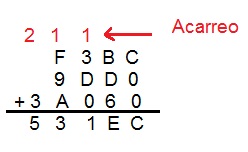
- 4AFC9 – DE8
Primero, el minuendo y el sustraendo deben de tener la misma cantidad de números. Por esto, añadiremos 0 para que ambos tengan la misma cantidad
4AFC9 – 00DE8
Luego, debemos de crear un nuevo número con la misma cantidad de números que posee el sustraendo. Este debe ser el mayor del sistema hexadecimal, que al ser 15 corresponde a la letra F. La resta se hace siguiendo las normas generales, con cada valor que corresponde a cada letra a operar.
FFFFF – 00DE8 = FF217
Ahora deberemos de sumar el minuendo y el complemento a 15 obtenido recientemente, utilizando la suma en sistema hexadecimal.
A4FC9 + FF217 = 14A1E0
Este resultado claramente no es el final ya que posee más números que al comienzo. Debemos de quitar el número de la izquierda (en este caso es el 1) y sumarlo.
4A1E0 + 1 = 4A1E1
Por lo tanto, 4AFC9 – DE8 es 4A1E1
-
-
Muchas gracias por el comentario Sebastian, efectivamente voy a revisar nuevamente el ejemplo por las dudas Muchas gracias!
-
-
Chicha dice: es como se menciona arriba, la resta hexadecimal no esta bien, el resultado deberia ser 4A1E1. Dado que es una pagina que explica eso pienso que si que deberias corregirlo, estuve bastante tiempo trantando de entender porque me daba otro resultado.
SAludos y gracias por la pagina
- Cristian Veloso dice:
Tienen razón, lo vamos a corregir en breve, gracias por la observación.
Saludos!
-
- Guillermo dice:
hola! podes creer que un profesor se está basando en estos ejemplos para enseñar este tema, y el error que mencionan en otro comentario lo confunde... no lo podrás corregir? de alguna manera el hecho de que esté mal, desinforma un poco 🙁
- Cristian Veloso dice:
hola Guillermo, tienes razón.
Lo voy a corregir en breve.
Gracias por el aporte.
-
Chicha 
Guillermo Deja un comentario
Hola, muchas gracias por compartir de sus conocimientos me ayudo mucho y entendi a la perfeccion. Hizo el trabajo de explicar muy bien.
Quiero tambien comentarle que en la operacion de la resta vi un error, cuando le va a sumar el minuendo al complemento a 15, (A4FC9-FF217) me doy cuenta que cambia el valor del minuendo original de la operacion inicial (4AFC9-DE8). O sea es decir 4AFC9 es indiferente a A4FC9.
Si continuamos la operacion de la resta con el valor original del minuendo de la operacion inicial, seria asi:
4AFC9-FF217
=14A1E0 Quitamos el numero de la izquierda ( en este caso el 1) y lo sumamos
4A1E0 + 1
= 4A1E1 Siendo este el valor real de la resta.
Lo comprobe pasando los numeros a valores decimales
4AFC9(base16) = 307145(base10) DE8(base16) = 3560(base10) 4A1E1(base16) = 303585(base10)
307145(base10) - 3560(base10) = 303585(base10)
Lo importante es que explico muy bien el procedimiento lo felicito, entendi mucho el procedimiento.
Si me equivoco en algo me avisa.
Gracias saludos.